Transient dynamics in the Edwards-Wilkinson model
We study the Langevin dynamics of an interface within the Edwards-Wilkinson model (or equivalently the Rouse chain model for a polymer). We develope a functional Fokker-Planck approach in order to study the effect of pinning of a single monomer and the effect of killing of the monomer (absorption).
- Shamik Gupta, Alberto Rosso and Christophe Texier,
Dynamics of a tagged monomer: Effects of elastic pinning and harmonic absorption
Phys. Rev. Lett. 111, 210601 (2013)
cond-mat arXiv:1308.0284.
Distribution of the center of mass of interfaces
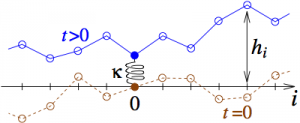
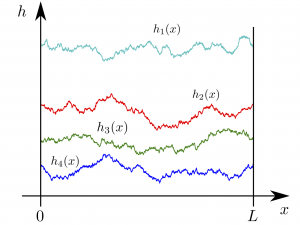
We consider a model of Brownian N non intersecting interfaces with a repulsive substrate. Nadal & Majumdar [Phys. Rev. E 79, 061117 (2009)] have studied the distribution of the position of the highest interface, h1, and also the distribution of the center of mass G=(1/N)Σi=1N hi.
In this article we consider the distribution of the fraction κ=N1/N of top interfaces. Using a mapping on a random matrix problem (within the Laguerre ensemble) we are led to study the distribution of a truncated linear statistics of the eigenvalues of Wishart matrices.
- Aurélien Grabsch, Satya N. Majumdar and Christophe Texier,
Truncated linear statistics associated with the top eigenvalues of random matrices ,
J. Stat. Phys. 167(2), 234-259 (2017)
cond-mat arXiv:1609.08296
See also page “ Random matrix theory ”
Counting equilibria for a directed polymer in a random environment
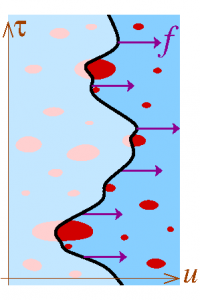
At T=0, an elastic line in a disordered medium submitted to a uniform force field is pinned by the disorder for a force below a critical threshold fc. We consider this problem by studying the average number of equilibria (stable or unstable).
We establish an interesting connection between the counting problem and the Anderson localisation of wave by a random potential.
- Yan V. Fyodorov, Pierre Le Doussal, Alberto Rosso and Christophe Texier,
Exponential number of equilibria and depinning threshold for a directed polymer in a random potential,
Ann. Phys. 397, p. 1-64 (2018)
cond-mat.dis-nn arXiv:1703.10066