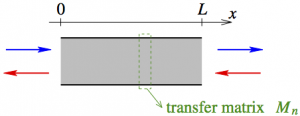
The study of a wave equation in an inhomogeneous medium, such as an electronic wave in a metallic wave guide, may be formulated in terms of transfer matrices. Within this frame, the analysis of 1D or quasi-1D (multichannel) random media leads to consider random matrix products:
(see page on 1D disordered QM). In particular, in 2010, we have found the connection between general matrix products in SL(2,R) and a model of generalised point scatterers:
- Alain Comtet, Christophe Texier and Yves Tourigny,
Products of random matrices and generalised quantum point scatterers
J. Stat. Phys. 140, 427-466 (2010)
cond-mat arXiv:1004.2415. - Alain Comtet, Christophe Texier and Yves Tourigny,
Lyapunov exponents, one-dimensional Anderson localisation and products of random matrices, [Review article]
J. Phys. A : Math. Gen. 46, 254003 (2013).
cond-mat arXiv:1207.0725
General products of random 2*2 matrices in the continuum limit (random matrices close to the identity)
We find analytical solutions for the Lyapunov exponent (i.e. the characteristic function) for most general products of random matrices of SL(2,R), in the continuum limit (matrices close to the identity).
Many of one-dimensional disordered problems may be mapped onto random matrix products. E.g. : Ising chain with random couplings and random magnetic field, in this case the Lyapunov exponent is interpreted as the free energy per site ; 1D quantum mechanics with disorder for which the Lyapunov exponent provides a measure of the localisation (precisely, the Lyapunov exponent is the inverse localisation length γ=1/ξ).
Our general formulation allows us to exhaust all possible 1D disordered models mapped onto random matrix products of SL(2,R) ; we have provided a classification of solutions (we recover known result and find several new solvable cases) that can be understand as a classification of 1D continuum disordered models.
- Alain Comtet, Jean-Marc Luck, Christophe Texier and Yves Tourigny,
The Lyapunov exponent of products of random 2*2 matrices close to the identity,
J. Stat. Phys. 150, 13-65 (2013).
math-ph arXiv:1208.6430
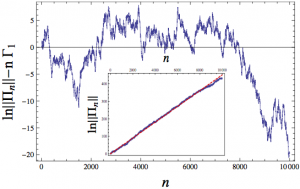
Fluctuations of random matrix products of SL(2,R) : Generalised Lyapunov exponent
Besides the study of the Lyapunov exponent, which characterises the average of the logarithm of a product of random matrices, the fluctuations may also be of interest: several motivations from physics are: the question of Single Parameter Scaling, the analysis of conductance fluctuations, etc. The study of fluctuations requires to study the generalised Lyapunov exponent or its expansion (cumulants):
Λ(q) = limN→∞(1/N) ln<||ΠN||q>
- Kabir Ramola and Christophe Texier,
Fluctuations of random matrix products and 1D Dirac equation with random mass,
J. Stat. Phys. 157, 497-514 (2014)
cond-mat arXiv:1402.6943
Some integral formulae for the variance are obtained, for few specific cases of random 2*2 matrices. - Christophe Texier,
Fluctuations of the product of random matrices and generalized Lyapunov exponent,
J. Stat. Phys (2020)
cond-mat arXiv:1907.08512
A general formalism is developed for any random matrix product of SL(2,R) - Christophe Texier,
Generalized Lyapunov exponent of random matrices and universality classes for SPS in 1D Anderson localisation,
Europhys. Lett. 131, 17002 (2020)
cond-mat arXiv:1910.01989
Using the general formalism of the previous article, the Single Parameter Scaling for Anderson localization is proven within a general framework, and extended to potentials with large fluctuations (such that <V2>=∞) - Alain Comtet, Christophe Texier and Yves Tourigny,
Representation theory and products of random matrices in SL(2,R),
math-ph arXiv:1911.00117
It is shown how concepts of representation theory can be used for the study of random matrix products and disordered systems.
The multichannel (quasi 1D) case : random matrix products in the chiral symmetry classes and the Dirac equation with a random matrix mass
- Aurélien Grabsch and Christophe Texier,
Topological phase transitions in the 1D multichannel Dirac equation with random mass and a random matrix model,
Europhys. Lett. 116, 17004 (2016)
cond-mat arXiv:1506.05322
We have studied the Dirac equation for N channels with a random (matricial mass). This corresponds to studying certain random matrix products of the symplectic group Sp(N,R) in the continuum limits.
cf. page “ 1D-disordered systems ” for details