Confronting the predictions of general relativity and quantum mechanics, Hawking showed in 1973 that black holes are not completely black, but emit a faint radiation. However, this radiation is too weak to be detected in the astrophysical context. We can circumvent this difficulty because we are now able to realize analogous systems in the lab: the flow of some quantum fluids emit a sonic analogue of the Hawking radiation.
In a series of works I participated to theoretically analyze some experimental platforms making it possible to realize an analogous black hole in a quantum fluid known as a « Bose-Einstein condensate ». See a popularizing note on entanglement in acoustic Hawking radiation and also a short movie (in french) by R. Drot and M. Relid (service communication de l’Université Paris-Sud) on acoustic black holes, from which the picture below is extracted.
| Although they widely differ in intensity and wavelength, the light emitted by a usual star and the Hawking radiation of a gravitational black hole have an important feature in common: their spectra are both fixed by their surface temperature and obey the so-called Planck’s law.In a work together with Mathieu Isoard, we theoretically reproduce recent experimental results and challenge their interpretation by arguing that, at variance with what occurs in a gravitational black hole, the analogous radiation of a Bose-Einstein condensate is not planckian. We also propose an experimental verification of this claim. |
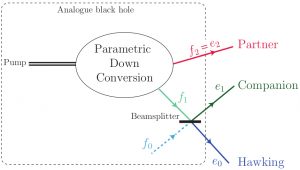
In a work with M. Isoard, N. Millazo and O. Giraud we studied bi- and tri-partite entanglement in an analog black hole realized in a Bose-Einstein condensate. The description of the localization of entanglement in the system suggests a quantum circuit model for the analog system: A parametric down-conversion process (e.g. triggered by a classical pump incident onto a nonlinear crystal) generates a two-mode squeezed vaccum state. One of the modes is the Partner, the other being sent on a beam-splitter generates the Hawking mode and a new mode (typical in dispersive analogues) we denote as Companion. See Fig. below:
This model suggested a new way to define the analogue Hawking temperature, yielding a result in much better agreement with the gravitational paradigm than previous definitions. Details in PhysRevA.104.063302