T-I-2draft

Linear response theory and Kramers-Kronig relations

The goal of this homework is to introduce the theory of linear response and, among the related properties, such as causality, the so-called Kramers-Kronig relations. We will consider the damped harmonic oscillator as a prototypical example to discuss this topic.

Reminder on the Fourier transform

Throughout this assignment, we will use the symmetric convention of Fourier transform. The Fourier transform of a function $f(t)\in L^{1}(\mathbb {R} )$ is defined as:

${\widehat {f}}(\omega ):={\frac {1}{\sqrt {2\pi }}}\int dt\,f(t)\,e^{i\omega t}.$

With this convention, the Fourier transform of a product results in a convolution, with the following pre-factor: ${\sqrt {2\pi }}\,{\widehat {(f\,g)}}={\widehat {f}}\ast {\widehat {g}}.$

The repeated application of the transform gives ${\widehat {\widehat {f}}}(t)=f(-t).$

The conjugate of a Fourier transform is equal to the transform of the conjugate, with a change of sign in the argument: ${\overline {\widehat {f}}}(\omega )={\widehat {\overline {f}}}(-\omega ).$

Furthermore, we can exchange the Fourier transform under the integral sign: $\int _{\mathbb {R} }dt\,{\hat {f}}(t)\,g(t)=\int _{\mathbb {R} }dt\,f(t)\,{\hat {g}}(t).$

The last property implies the result $\int _{\mathbb {R} }d\omega \,{\overline {\hat {f}}}(\omega )\,{\hat {g}}(\omega )=\int _{\mathbb {R} }dt\,{\overline {f(t)}}\,{\hat {g}}(t),$ which gives directly the Plancherel theorem (see lecture notes, page 45).

Example: damped harmonic oscillator in one dimension

We consider a damped harmonic oscillator $x(t)$, which is described by the following equation of motion:

${\ddot {x}}+2\gamma \,{\dot {x}}+\omega _{0}^{2}\,x=f(t).$

First, we will compute its response to an harmonic perturbation, and then its response to a generic perturbation by introducing its Green function.

Response to an harmonic perturbation

We assume that the oscillator is excited by an harmonic perturbation of the form: $f(t)=F_{\omega }\,e^{-i\omega t}.$ We look for a solution of the form: $x(t)=X_{\omega }\,e^{-i\omega t}.$

Q1: Show that

$X_{\omega }={\hat {g}}(\omega )\,F_{\omega },$

where

${\hat {g}}(\omega )=-{\frac {1}{(\omega -\omega _{1})(\omega -\omega _{2})}}.$

Write the explicit form of the poles that we have indicated as $\omega _{1}$ and $\omega _{2}$.

Response to a generic perturbation

We consider a generic perturbation represented by $f(t)$, whose Fourier transform is given by ${\hat {f}}(\omega )$.

Q2: Write $x(t)$ as a function of ${\hat {g}}(\omega )$ and ${\hat {f}}(\omega )$.

Q3: Show that it follows that

$x(t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }dt'\,g(t-t')f(t'),$

where $g(t)$ is the function having ${\hat {g}}(\omega )$ as Fourier transform. The above equation is nothing but the convolution of $f$ with $g$: ${\sqrt {2\pi }}x(t)=(f\ast g)(t)$.

Holomorphism of the response and consequences

Q4: Show that $g(t)$ is the response of the system to an impulsive perturbation $f(t)={\sqrt {2\pi }}\delta (t)$. What is the effect of a perturbation applied at time $s$ on the solution at time $t<s$?

Q5: We have defined ${\hat {g}}(\omega )$ for $\omega \in \mathbb {R}$, i.e. on the real axis. Show that its extension to the complex plane is holomorphic everywhere (except at the poles). Using the explicit expression for ${\widehat {g}}(\omega )$ derived above, compute explicitly $g(t)$. You will have to treat separately the case of positive time and the case of negative time. Use the residue theorem.

Q6: Deduce the expression of the response:

$x(t)=\int _{-\infty }^{t}dt'\,e^{-\gamma (t-t')}\,{\frac {\sin \left[(\omega _{0}^{2}-\gamma ^{2})^{1/2}(t-t')\right]}{(\omega _{0}^{2}-\gamma ^{2})^{1/2}}}f(t').$

The above expression indicates the Green function of the system. Notice that the response of the system is causal.

It is worth highlighting the importance of the holomorphism in this proof. Indeed, we have seen that we had to apply Jordan's lemma. Therefore, we need a relatively fast decay of the response function at infinity, i.e. a system that does not diverge.

We also point out that, if $\gamma$ was negative, we would have lost causality: we can guess a relation between causality and the dissipation of energy in a passive system.

General properties of linear response

We look for a generalization of the properties that we have seen in the previous example. We discuss an equation of motion (or possibly another physical equation)

${\mathcal {L}}x(t)=f(t),$

with a linear operator ${\mathcal {L}}$ (of differentiation, multiplication, integration, etc.), and with an inhomogeneity $f(t)$ (external stimulation, perturbation, etc.). The generic solution is unknown since the explicit form of the operator is not specified. However, we know that this solution must have some physical properties:

• Linearity: $x$ is a function or a linear functional of $f$, which reads $x(t)=\int _{\mathbb {R} }ds\,g(t-s)f(s).$
• Causality: in the sense that the effect cannot precede the cause: $g(t)=0$ for $t<0$.
• The total response to a finite perturbation must be finite.
• The response to a real perturbation, $f(t)\in \mathbb {R}$, must be real as well, $x(t)\in \mathbb {R}$ (at least in the case we are not considering quantum mechanics effects).

Link between odd/even and real/imaginary

Q7: Show the following properties of the Fourier transform:

• if $g\in \mathbb {R}$ is an odd function, then ${\hat {g}}\in i\mathbb {R}$ is also an odd function;
• if $g\in i\mathbb {R}$ is an odd function, then ${\hat {g}}\in \mathbb {R}$ is also an odd function;
• if $g\in \mathbb {R}$ is an even function, then ${\hat {g}}\in \mathbb {R}$ is also an even function;
• if $g\in i\mathbb {R}$ is an even function, then ${\hat {g}}\in i\mathbb {R}$ is also an even function.

Q8: Conclude that, if $g$ is real, its Fourier transform is written as ${\hat {g}}={\hat {g}}'+i{\hat {g}}''$, with ${\hat {g}}'$ even, and ${\hat {g}}''$ odd.

Q9: Derive the same properties for the case of the oscillator.

Preliminaries

We define the sign function as

$S(t)={\begin{cases}-1&t<0\\+1&t\geq 0\end{cases}},$

and we want to show that its Fourier transform is

${\hat {S}}(\omega )={\sqrt {\frac {2}{\pi }}}{\frac {i}{\omega }}.$

Since $S$ is not summable, we have to use an auxiliary function $S_{\epsilon }(t):=e^{-\epsilon |t|}S(t)$.

Q10: Show that $\lim _{\varepsilon \rightarrow 0}{\hat {S}}_{\epsilon }(\omega )={\sqrt {\frac {2}{\pi }}}{\frac {i}{\omega }}$.

Q11: Discuss the possibility of using ${\hat {S}}$ instead of ${\hat {S}}_{\epsilon }$ in a computation (e.g., in the example below).

Causality and Kramers-Kronig relations

Q12: Using the expression of the Fourier transform of a convolution and the sign function defined above, show the following property of Fourier transform:

If $g(t)=0$ $\forall t<0$, then $\quad {\hat {g}}(\omega )={\frac {1}{i\pi }}\,{\rm {PV}}\int _{\mathbb {R} }d\xi \,{\frac {\operatorname {Im} {\hat {g}}(\xi )}{\xi -\omega }}$.

By separating the real and imaginary part of this equation, we obtain Kramers-Kronig relations:

$\operatorname {Re} {\hat {g}}(\omega )={\frac {1}{\pi }}\,{\rm {PV}}\int _{\mathbb {R} }d\xi \,{\frac {\operatorname {Im} {\hat {g}}(\omega )}{\xi -\omega }},$ $\operatorname {Im} {\hat {g}}(\omega )=-{\frac {1}{\pi }}\,{\rm {PV}}\int _{\mathbb {R} }d\xi \,{\frac {\operatorname {Re} {\hat {g}}(\omega )}{\xi -\omega }}.$

Q13: Show that Kramers-Kronig relations express the fact that the extension ${\hat {g}}(\omega +i\nu )$ to ${\hat {g}}(\omega )$ on the complex upper-half plane $(\nu >0)$ is holomorphic, without any poles, and that it decreases sufficiently fast as $|\omega +i\nu |\rightarrow \infty$.

We will start from a weaker result:

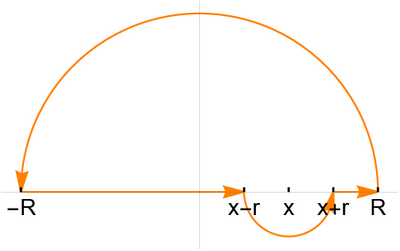
Show that the Kramers-Kronig relation is valid for all functions ${\hat {g}}(\omega +i\nu )$ with the aforementioned properties. Apply the residue theorem integrating along the path $\gamma$ displayed in the figure below, that can be reproduced via the following code:

gamma = ParametricPlot[{{R Cos[t], R Sin[t]}, {-R*(1 - t/Pi) + (x - r)*t/Pi, 0}, {r Cos[t + Pi] + x, r Sin[t + Pi]}, {(x + r)*(1 - t/Pi) + R*t/Pi, 0}} /. {R -> 2,  r -> 0.5, x -> 1}, {t, 0, Pi}, Ticks -> {{{-R, "-R"}, {x - r, "x-r"}, {x, "x"}, {x + r, "x+r"}, {R, "R"}} /. {R -> 2, r -> 0.5, x -> 1}, None}, TicksStyle -> Directive[Red, 20], AxesLabel -> {None}] /. Line[u_] :> Sequence[Arrowheads[Table[.05, {1}]], Arrow@Line[u]]

Sketch of the integration path $\gamma$.

Integrate the function ${\hat {g}}(z)/(z-\omega )$ along this path. Compute the contribution of the small half-circle $C_{r}$ in the limit $r\rightarrow 0$ using its Taylor expansion in the vicinity of $\omega$ and performing the change of variable $z'=\omega +r\,e^{i\theta }$.

The last result suggests the existence of a relation with the causality at $g(t)=0$ $\forall t<0$ and the fact that $g$ is holomorphic without poles in the upper-half plane. This was detailed in the Titchmarsch theorem.